スマートニュースの高橋力矢です。去る3月5日(日)に、電気通信大学で開催されたゲーム理論ワークショップに出席しました。そこで機械学習とゲーム理論とのつながりについて経済学者や生物学者の方々と話してきましたので、当日議論したことをここでも紹介したいと思います。当日のプログラムはこちらで見られます。今回の講演に当たっては電気通信大学の岩崎敦先生に大変にお世話になりました。この場を借りまして改めて御礼申し上げます。以下にプレゼンテーション資料も添付しましたので、数式や参考文献等の技術的詳細に興味ある人はご覧ください。
要旨とスライド
- 複数のプレイヤーが利害を持つ環境における社会現象や最適戦略の分析にはゲーム理論が役立つ
- ゲーム理論的分析には利得表が必要であり、その具体的数値の取得にはデータ分析が有効である
- しかしデータ分析による利得表には誤差が伴い、誤差の水準によっては結論が変わりえる
- データ分析(帰納)の後にゲームを解く(演繹)よりも、両者を統合した単一問題を解く方がよい
- その単一問題は、個別の帰納問題・演繹問題よりも簡単に解けることがある
ゲーム理論のためのデータ分析
私たち人類の行う意思決定による利得と損失は、自分の選択だけでなく他人の行動にも左右されます。例えば広告投資について考えましょう。広告出稿による獲得顧客数といったマーケティングKPIは、自社広告だけでは決まらず競合他社の広告によっても変化します。競合他社の動きが読めないと自社の戦略が決められない事態に直面するわけです。自社も他社も戦略的に広告投資を行っている状況で、他社はどのような投資を行うと想定すべきで、自社の最適戦略は何でしょうか? この問いに対する答えは例えば(Naik et al, 2005)で深く議論されており、その定式化・計算にはゲーム理論やその親戚であるマルチエージェント・シミュレーションが使われます。
ゲーム理論的分析には利得表と呼ばれる全プレイヤーの戦略と利得との対応表が必要です。この利得表が入力として与えられるとゲーム理論家または計算機が「ゲームを解き」、各プレイヤーごとの均衡戦略が出力として得られます。ゲームを解く際には、各プレイヤーは「他のプレイヤーが最適戦略を選択していると考えた上で自分の最適戦略を選ぶ」という仮定がよく用いられます。つまり均衡戦略は、皆が先読みをしている社会を想定した場合に、起き得る可能性の高い社会状況を指しています。
利得表をデータ分析により与えるとしましょう。広告戦略の実務の場合、利得表は自社・他社それぞれの戦略と対応する各社のKPIの実現値からなります。データサイエンティストは、自社の過去の投資額を説明変数、KPIを従属変数とした回帰分析から仕事を始めるでしょう。広告に限らずダイレクトメール等の個別販促もふくめることで、自社のマーケティング・ミックスであれば個人顧客の属性まで含めた詳細な分析も可能です。一方で競合他社の動向については、過去に打たれたテレビCM等マス広告に関するデータ収集が関の山です。これで競合他社のテレビCMと自社の売上との回帰分析はできますが、その回帰係数が分かっても競合他社が将来どれだけ投資するか分からないと自社の戦略策定に役立ちません。回帰分析だけで仕事を終わらせず、推定した利得表をゲーム理論家に渡しましょう。想定すべき他社の戦略がわかり、自社の最適戦略を立てられるようになります (*)。
(*)のお勧めに納得しない読者はセンスのある人物だと思います。データ分析を利用してゲームを解く場合、使われる利得表が誤差つきの推定値にすぎない点が大きな問題となります。誤差が発生する理由はサンプルサイズの有限性です。推定値+誤差を確率分布で表現すると不確実性を定量化することができ、頻度論ならば信頼区間、ベイジアンなら信用区間で与えられます。利得表に関する不確実性の有無がゲーム理論からのインプリケーションを変えてしまうことがあるため、推定された利得表の誤差に由来する判断の誤りは防がなければいけません。どのような方法が取れるでしょうか。
利得表の推定を精密にした上で、限りなく正確にゲームを解くべきでしょうか。そのような一見正確性を重視したアプローチは、実際にはお互いが必要以上に頑張ってしかも部分最適な戦略を手にいれる不毛であると私は考えます。代わりにデータ分析とゲーム理論を統合した一つの問題だけを解くのはいかがでしょうか。このとき、統合された問題が 簡単に解ける場合があるというのがポイントで、強化学習の例を用いて後述します。データサイエンティストとゲーム理論家はお互いの分業を否定して双方の分野を学ぶべきです。しかし双方の考え方をそのままくっつけるのではなくて、より簡単な別の問題を創り出すことがデータに基づく良い意思決定の鍵です。コンセプトとしては図1のようになります。
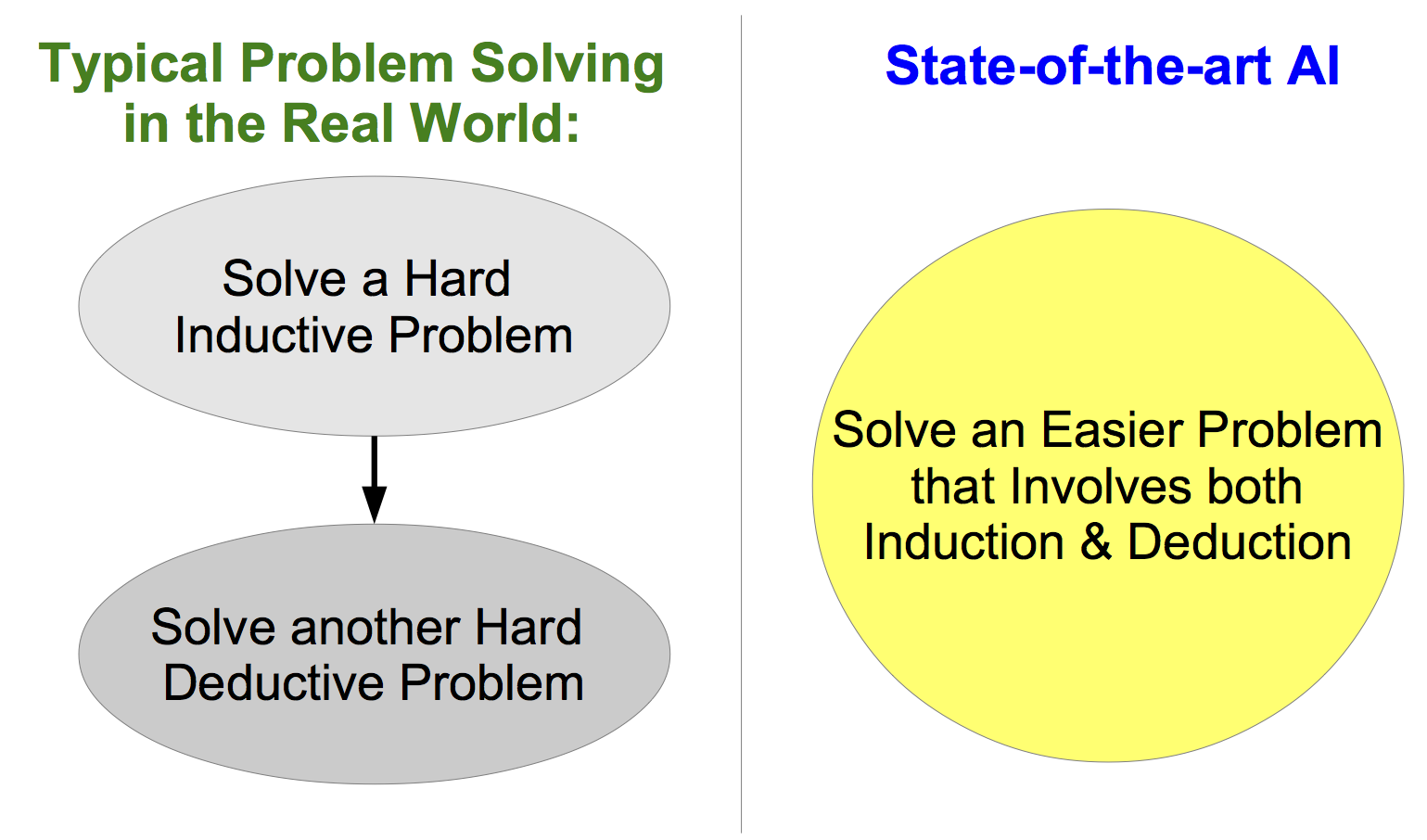
図1. 帰納と演繹と統合した一つの問題を解く (コンセプト)
帰納と演繹とで分業しない
図2をご覧ください。図2左は第1ステップであるデータ分析の後に第2ステップであるゲーム解決 or 意思決定を行う、シーケンシャルで典型的なアプローチを示しています。一方で図2右はデータから直接意思決定するアプローチを示しています。図2右においても今までのデータ分析同様に、利得表に関連した推定値$\check\Theta_{\mathcal D}$は得られます。しかしこの推定値は、第1ステップで得られた精密な利得表推定値$\widehat\Theta_{\mathcal D}$とは違って、推定値自体の誤差は必ずしも最小化されておらず、むしろ誤差の最小化を意図的に避けた値が使われたりします。いわば「さぼった推定値」です。意思決定の品質を上げたいならばデータサイエンティストは真面目に統計的推定を行ってはならないという本業否定みたいな話ですが、その根拠を理解するために、ここからは話をゲーム理論に限らずあらゆる種の意思決定に一般化して議論しましょう。
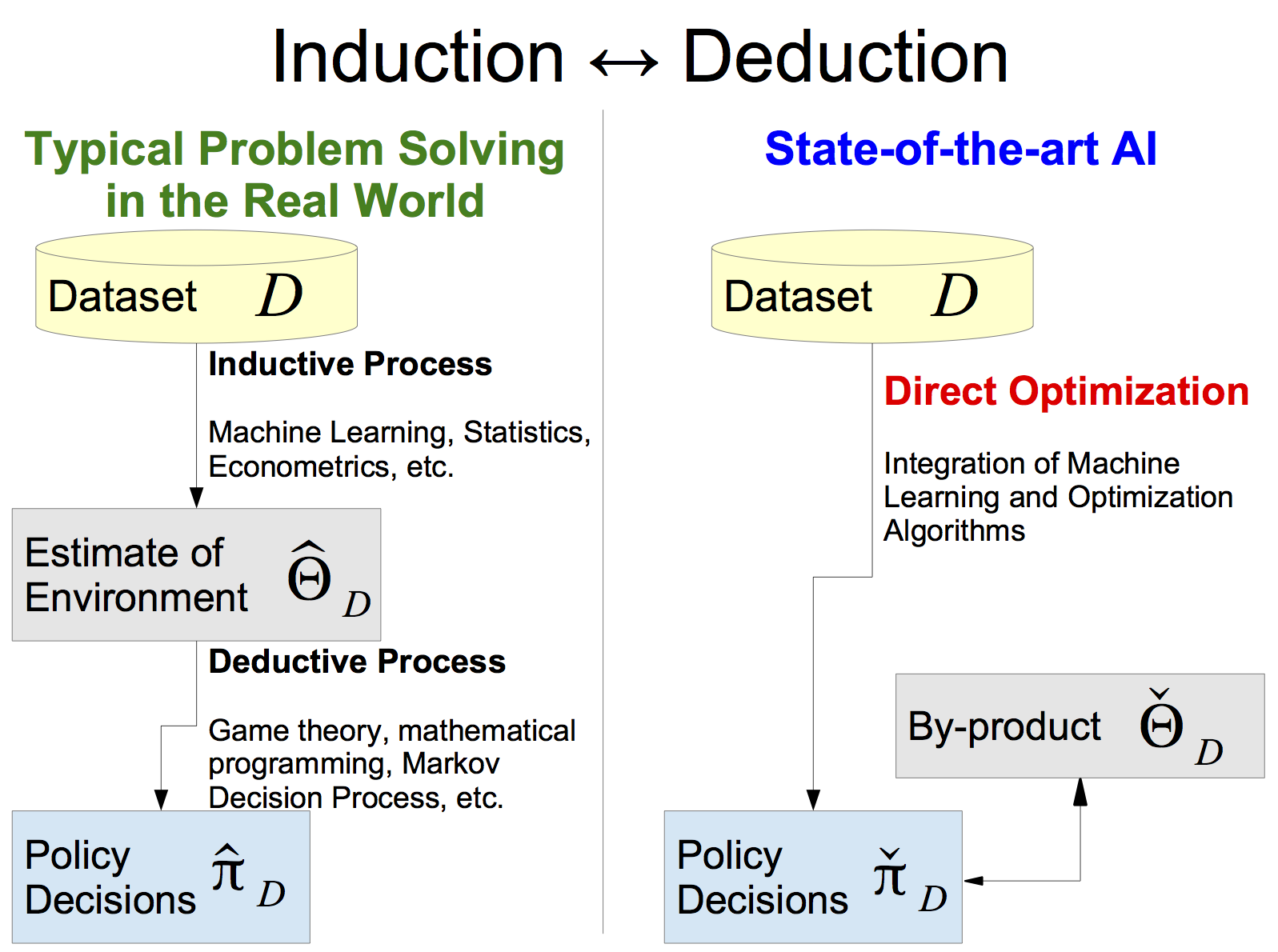
図2. 帰納と演繹と統合した一つの問題を解く (推定値)
統計学者や機械学習家、計量経済学者は、未知の環境に関する情報を有限のデータから精密に推定します。単純化して言えば、彼らは帰納の専門家です。一方で、ゲーム理論家やオペレーションズ・リサーチの研究者は演繹の専門家と言えます。彼らは環境の性質が与えられたときに最適戦略が何であるか導出するのが得意だからです。広告競争の例に限らず、帰納専門家の推定結果を利用して演繹専門家が意思決定を行う or 発生しうる社会状況を列挙するという分業は実務でしばしば発生します。
このような分業が正当化される場合、1人が全ての専門分野を学ぶよりも各人が異なる得意分野に集中する方が効率的であることが根拠になります。経済学ならRicardoの比較優位という考え方があります。各人が最も得意な仕事に集中することで全体の生産性が上がると示唆されますし、各人が他者に対して絶対的に勝るスキルを持っていなくても構わない点が強調されます。より主観的な見解では、複数の専門分野にまたがるスーパースターになるのは大変で無理だから止めなさいという諦めもあるでしょう。
しかし複数の専門分野にまたがった問題の方が簡単に解けるならば、話が変わってきます。わざわざ問題を分けてそれぞれのパートで複雑な解法を用いるのは賢くありません。そのことを理解する良い代表例として、近年のDeep Q-Network (Mnih, 2015)やAlphaGo (Silver et al., 2016)に代表される強化学習技術を取り上げます。強化学習では帰納と演繹を統合した一つの問題を解きます。
MDP推定をさぼるQ学習、Q学習すらさぼる方策勾配法
たとえば広告によるブランド醸成のように、施策による利得が時間的に遅れて発生する状況で最適戦略を求める場合、マルコフ決定過程 (Markov Decision Process; MDP)が使われます。MDPの環境が分かっている場合、最適戦略は動的計画法か線形計画法により簡単に求まります。MDP環境下の最適意思決定問題を、環境が未知の場合に解く技術を総称して強化学習と言います。強化学習はModel-basedアプローチとModel-freeアプローチに大別されます。
- Model-based: MDPのパラメータを統計的推定し、推定されたMDPを解いて意思決定する
- Model-free: MDPのパラメータを推定せずに、方策の最適化だけに焦点を当てる
ベーシックなMDPの場合、環境のうち推定すべきパラメータは行動$a$をとったときに状態$s$から状態$s’$に遷移する確率 $P(s’ \vert s,a)$ と状態$s$で行動$a$をとったときの直近報酬の期待値$r(s,a)$です。離散状態・離散行動の場合、状態遷移確率は要素数が(状態数)$^2$$\times$(行動数)のテーブルで表現されます。しかし要素数が(状態数)$\times$(行動数)のテーブルである状態行動価値関数$Q(s,a)$だけ分かれば最適意思決定ができることが、ベルマン最適方程式から示唆されます。状態行動価値関数$Q(s,a)$は、状態$s$にいた場合には行動$a$を選択する、という方策を一貫して続けた場合の累積報酬期待値です。
Model-free学習の一つであるQ学習では、真の環境 $\lbrace P(s’ \vert s,a), r(s,a) \rbrace$を知る代わりに$Q(s,a)$だけ推定して意思決定します。この「さぼった推定」の便益、つまり推定された最適方策に関する精度は、状態$s$や行動$a$の次元が上がるほどModel-basedに比べて顕著になります。状態$s$や行動$a$が高次元ベクトルである場合のQ学習はFitted $Q$-Iteration (Ernst et al., 2005) 以降脈々と進化し、関数近似にDeep Convolutional Neural Networkを用いた今日のDeep Q-Networkにつながっています。
Q学習を可能にした「さぼった推定」のアイデアは更に活用することができます。簡単な問題として、いずれも現在株価が\$100の3種類の株式A, B, Cのうち、どれか1種類に全ての資金を投資する状況を考えましょう。分散ポートフォリオは考えないものとします。それぞれの株価の1年後の期待値がA:\$90, B:\$100, C:\$120だと、仮に予測できたとします。ボラティリティはA,B,C全て同じで±\$20です。どの株式を買うべきでしょうか? 答えはCですね。では期待値がA:\$90, B:\$100, C:\$110だった場合はどうでしょうか。やはり合理的選択はCです。Cの期待価格が\$120でも\$110でも最適戦略は変わりません。
仮想株式の単純な例が示唆する事は、最終的に知りたいのは状態$s$で行動$a$を取るべき確率$\pi(a|s)$であって、そのためには$Q(s,a)$さえも推定誤差を許容して良いということです。この考えを拡張すると方策勾配法による強化学習ができます。REINFORCE (Williams, 1992)アルゴリズムや、より発展形のActor-Criticアプローチでは$\pi(a\vert s)$の推定精度を最大化することに力を注ぎます。$Q(s,a)$についてはその相当値を推定はしますが、その際に「さぼった」推定を行うため必ずしも誤差を最小化しません。特にREINFORCEアルゴリズムでは過去に観測された報酬の合計を使うというかなり乱暴なことをやります。
- 注: Actor-Criticの場合は方策勾配の推定値をunbiasedにするために最小二乗誤差推定を行います
一般的に支持されている見方は、方策勾配法は確率分布$\pi(a\vert s)$をうまくパラメトライズすれば行動$a$が連続値ベクトルでも適用できて都合が良いというものです。これはもちろん真ですが、方策勾配法の真価は最終目的変数の最適化にダイレクトに焦点を当てている点だと思います。有限サンプルの場合、得られる全てのパラメータ推定値に誤差が乗っています。誤差を全てゼロにすることはサンプル数が無限大の場合、または真の環境が決定的な場合しかできませんので、確率的環境で有限サンプルである限りはどのパラメータの誤差をもっとも重視するのか選ばなければなりません。離散の場合$Q(s,a)$と$\pi(a\vert s)$のパラメータ数はどちらも(状態数)$\times$(行動数)で同じに見えますが、$\pi(a\vert s)$の推定誤差と$Q(s,a)$の推定誤差と、どちらを優先するのかで意思決定の品質は変わってしまうわけです。意思決定の品質がもっとも重要である限り、最小化すべきは方策$\pi(a\vert s)$の推定誤差になります。
そもそも環境を知る必要があるのか
強化学習アルゴリズムからの示唆は、私たちの典型的なものの考え方に疑問を投げかけます。端的に言って私たちの脳は、最終的なアウトプットである意思決定の品質を下げるやり方をわざわざ好むように見えます。帰納と演繹を分けることでかえって誤差を拡大してしまう過ちは、本質的には以下の誤謬もしくは認知バイアスが引き起こしているように見えます。さらに分業体制は、それぞれのパートで不必要に労力をかけてしまう部分最適性も生み出します。
- 1. 環境を「理解したい」という欲求のために中間的な推定を行ってしまい、不要な誤差を付加する
- 2. 分析結果を「見る」ときに誤差や不確実性を把握せず真の環境を知ったかのように錯覚する
- 3. 中間推定値の誤差を下げることで、最終的な意思決定の誤差を上げてしまう。有限サンプル下では各推定値の間にトレードオフがあることを忘れている
上記の誤謬2に関して。誤差つきの推定値を決定値のようにみなして過剰な解釈をする傾向はNarrative Fallacyの一種と言えるかもしれません。現実のデータ分析結果を正直に説明した場合、ある施策は効果がありそうに見えるけど信用区間から見るに推定の間違いの可能性も高い、といった曖昧な結論になったりするのです。このような不確実性を無視してストーリーのある説明を過剰に信頼すると、結果的には最終的な意思決定の品質を落としてしまいます。
上記のそれぞれの誤謬は、帰納と演繹との分離だけでなく、あらゆる種の分業で起きていることでしょう。各モジュールを分けてプロダクト開発を行っているエンジニア達が、それぞれの開発工程に不必要に頑張り過ぎて疲弊することはないでしょうか。この誤りは各担当者の責任ではなくて、モジュールに分割する事前のマネジメント・意思決定に由来するものです。プロセスA+B+C+D+Eによってプロダクトを作っているところを、それらのどれとも違う一つの簡単なプロセスXによって代替することを常に検討すべきでしょう。皆様の今後の重大な意思決定において、上記リストの誤謬2は覚えておくと役立つと思います。データ分析+ゲーム理論の枠にとどまらない広範な問題です。
一方で、環境が完全には分からなくても戦略が合っていれば良いという割り切りは、経験の深いビジネスパーソンなら納得するかもしれません。お客様が本当は何を欲しがっているのか、あるいはなぜ特定の商品を買うのか完全にわかる売り手はいません。しかし売り手がお客様にお勧めした商品が、結果的にお客様の意向に沿ったものであれば真の購買動機がわからなくても取引は成立します。購買の理由を推測することは今後の商品開発にとって有益ではありますが、推測自体を目的とする必要はありません。中間推定値としての利得表はある程度は知りたいけど、利得表の推定精度自体を最適化する必要はないという点と同一ですね。
有限の計算能力は常に不確実性を生み出す
ゲーム理論ワークショップでは印象に残った面白い質問がいくつかありました。その一つは「囲碁はルールが決定的で麻雀のようにランダムネスが入る余地がない。なのに、なぜアルゴリズム上は不確実性を考慮する必要があるのか」というものです。恐らくは、この質問の背後では純粋に演繹的な囲碁の解き方が想定されていたと思います。純粋に演繹的とは、自分と相手の全ての先読みを明示的に計算・探索して最適な手をうつことです。しかしAlphaGoのようにExperience Replayを採用した強化学習アルゴリズムは探索をさぼるために帰納を利用しています。この帰納が不確実性の考慮を要求します。
囲碁や将棋といったゲームの探索には計算時間がかかるため、全ての手を調べることは実際にはできません。そこで、有限時間で探索した局面と手を元に、局面別の各手とスコアとの対応表を作ります。これがExperience Replayと呼ばれる記憶部分で、この対応表における回帰分析を行うことで探索しなかった局面・手についてもスコア推定値を与えられるようになります。何度も述べるように、スコア推定値は真のスコアからは乖離しています。計算が間に合わない部分を帰納的に補間することで早くて賢いプレイヤーを作り出しているわけですが、そのために用いた帰納的方法論が不確実性を呼び込みます。決定的なゲームでも計算の限界により不確実性が生まれる現象は、計算機だけでなく人が戦略をプレイする場合にも知っていて損はありません。
その他、関連技術について
最後に、興味ある読者のために、関連技術について一部の参考文献を上げておきます。冒頭に広告戦略の例を挙げましたが、ゲーム理論的環境を想定せず(競合他社の影響を無視して)、自社の広告費と獲得顧客との関係のみを分析する場合もMDPが使われます。マス広告のマーケティング・ミックスであれば(Naik and Raman, 2003), (Kumar et al., 2011), (Raman et al., 2012)などがあります。個別の個人消費者に対するダイレクト・マーケティングであれば(Elsner et al., 2003), (Abe et al., 2004), (Tirenni et al., 2007), (Gómez-Péreza et al., 2009), (Takahashi et al., 2014)などです。最後の自著研究は個人顧客のターゲティングと顧客ポートフォリオ全体の予算制約つき最適化を両立した問題を解いています。
ゲーム理論における、皆が先読みをしているという仮定自体は妥当と思われますが、無限遠まで先読みした前提で均衡を計算することについては議論の余地があります。囲碁や将棋では計算機も人間も有限の先読みしかしていません。しかし実社会では、ゲームを繰り返しているうちに無限遠を読んだ場合の戦略を結果的にプレイしていることもあります。先読み範囲を打ち切ることで実世界での表現能力を上げる研究としては認知階層理論 (Camerer et al., 2004) が有望です。また先読みできないことによる不確実性を明示的に確率的撹乱項として導入すると、通常のナッシュ均衡の代わりに質的応答均衡 (Quantal Response Equilibrium; QRE) (McKelvey and Palfrey, 1995)が表れます。認知階層理論、QREとも先読み能力(=最適化能力)に罰則項を設ける形になりますが、最適化能力に罰則項を設ける部分をベイズ的に定式化することで認知バイアスを再現するアプローチは私個人も研究しています (Takahashi and Morimura, 2015)。興味ある人はワークショップのスライドを追ってみてください。
自動運転やドローン制御のように、複数プレイヤー間の相互作用を考慮した機械学習・強化学習アルゴリズムは今後ますます発展するでしょう。これらのアルゴリズムにゲーム理論や経済学の視点を入れることで、人間の社会にとって本質的に必要な、洗練された意思決定手法を編みだせるかもしれません。このように、高度な機械学習を社会的問題解決に役立てることに関心のあるエンジニアの方は下記の求人もチェックしてみると、良い将来が待っているかもしれませんよ。
References
- P. A. Naik, K. Raman, and R. S. Winer, Planning marketing-mix strategies in the presence of interaction effects, Marketing Science, 25(1):25–34, Jan. 2005.
- V. Mnih, K. Kavukcuoglu, D. Silver, A. Rusu, J. Veness, M. Bellemare, A. Graves, M. Riedmiller, A. Fidjeland, G. Ostrovski, S. Petersen, C. Beattie, A. Sadik, I. Antonoglou, H. King, D. Kumaran, D. Wierstra, S. Legg, and D. Hassabis, Human-level control through deep reinforcement learning. Nature, 518:529–533, 2015.
- D. Silver, A. Huang, C. Maddison, A. Guez, L. Sifre, G. van den Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, S. Dieleman, D. Grewe, J. Nham, N. Kalchbrenner, I. Sutskever, T. Lillicrap, M. Leach, K. Kavukcuoglu, T. Graepel, and D. Hassabis, Mastering the game of Go with deep neural networks and tree search. Nature, 529:484–489, 2016.
- D. Ernst, P. Geurts, and L. Wehenkel, Tree-Based Batch Mode Reinforcement Learning, Journal of Machine Learning Research, 6:503–556, 2005.
- R. J. Williams, Simple statistical gradient-following algorithms for connectionist reinforcement learning. 8(3):229–256, 1992.
- P. A. Naik and K. Raman, Understanding the impact of synergy in multimedia communications, Journal of Marketing Research, 40(4):375-388, Nov. 2003.
- V. Kumar, S. Sriram, A. Luo, and P. Chintagunta, Assessing the effect of marketing investments in a business marketing context, Marketing Science, 30(5):924–940, Sep. 2011.
- K. Raman, M. Mantrala, S. Sridhar, and E. Tang, Optimal resource allocation with time-varying marketing effectiveness, margins and costs, Journal of Interactive Marketing, 26(1):43–52, Feb. 2012.
- R. Elsner, M. Krafft, and A. Huchzermeier, Optimizing Rhenania’s mail-order business through Dynamic Multilevel Modeling (DMLM), Interfaces, 33(1):50–66, Jan./Feb. 2003.
- N. Abe, N. K. Verma, C. Apte ́, and R. Schroko, Cross channel optimized marketing by reinforcement learning, in Proceedings of the 10th ACM SIGKDD Conference, 767–772, 2004.
- G. Tirenni, A. Labbi, C. Berrospi, A. Elisseeff, T. Bhose, K. Pauro, and S. Pöyhönen, The 2005 ISMS Practice Prize Winner–Customer Equity and Lifetime Management (CELM) Finnair case study, Marketing Science, 26(4):553–565, Jul./Aug. 2007.
- G. Gómez-Péreza, J. D. Martín-Guerreroa, E. Soria-Olivasa, E. Balaguer-Ballesterb, A. Palomaresb, and N. Casariego, Assigning discounts in a marketing campaign by using reinforcement learning and neural networks, Expert Systems with Applications, 36(4):8022-8031, May. 2009.
- R. Takahashi, T. Yoshizumi, H. Mizuta, N. Abe, R. L. Kennedy, V. J. Jeffs, R. Shah, and R. H. Crites, Multi-period marketing-mix optimization with response spike forecasting, IBM Journal of Research and Development, 58(5-6), 1:1-1:13, Nov. 2014.
- C. F. Camerer, T. H. Ho, and J. Chong, A cognitive hierarchy model of games, Quarterly Journal of Economics, 119(3), 861–898, 2004.
- R. McKelvey and T. Palfrey, Quantal response equilibria for normal form games, Games and Economic Behavior, 10(1):6–38, 1995.
- R. Takahashi and T. Morimura, Predicting preference reversals via gaussian process uncertainty aversion, In Proceedings of the 18th International Conference on Artificial Intelligence and Statistics (AISTATS 2015), 958–967, 2015.