こんにちは、スマートニュースの徳永です。深層学習業界はGANだとか深層強化学習だとかで盛り上がっていますが、今日は淡々と、畳み込みニューラルネットを高速化するための手法を紹介します。
量子化、スパース化と、ひらすらニューラルネットの話ばかり書いてきましたが、今回で一段落の予定です。だんだんと記述が雑になっていることを自分でも感じていますが、ちょっと疲れてきてるのでご容赦下さい。
ニューラルネットにおいて、畳み込み演算が非常に重要な地位を占めることは論を待ちません。画像認識においては畳み込みニューラルネットに匹敵する高精度な手法は他にありませんし、自然言語処理においても、最近、畳込みニューラルネットが注目を集めています。また、畳み込みは、音声認識や音声合成でも使われています。GoogleのTPUのワークロードでは、畳み込みニューラルネットは5%ぐらいしかないとの報告もありますが、とりあえず、この論文は見なかったことにして、話を進めましょう。
畳み込みニューラルネットの泣き所は膨大な計算量です。とりあえず手持ちのノートPC(GPUなし)で畳み込みニューラルネットを試してみて、計算が全然終わらなくて仕方なくGPUを買いに行った、みたいな経験をお持ちの方も多いのではないでしょうか。
Winogradアルゴリズム
Winogradアルゴリズムは小さいフィルターサイズ(3x3とか)の畳み込みを高速化するのに向いているアルゴリズムです。neonやcuDNNで使われています。
Winogradアルゴリズムを直感的に説明するのは難しいのですが、Fast Algorithms for Convolutional Neural Networksの例を元に、1次元の場合を少しだけ説明してみましょう。フィルタを$\mathbf{g} = (g_0, g_1, g_2)$として、畳み込まれるデータを$\mathbf{d} = (d_0, d_1, d_2, d_3)$とすると、畳込みの計算は、以下のような行列積の形で書けます。
この行列積をそのまま計算するのではなく、以下のように式変形します。
ただし、$m_1 = (d_0 - d_2) g_0, m_2 = (d_1 + d_2) \frac{g_0 + g_1 + g_2}{2}, m_3 = (d_2 - d_1) \frac{g_0 - g_1 + g_2}{2}, m_4 = (d_1 - d_3) g_2$です。
なにがなんだかわからない、という声がここまで聞こえて来るような気すらしますが、それはともかく、$m_1 + m_2 + m_3$に上記の定義を入れて計算すると、たしかに$d_0 g_0 + d_1 g_1 + d_2 g_2$が出てきます。
重要なのは乗算の回数で、もともとの行列積の形では6回の乗算がでてきましたが、変形後は4回に減っています。この1次元の例では代わりに加算減算が増えてしまってますが、2次元の場合について同様に計算すると、トータルでは効率が良くなる、というのがWinogradアルゴリズムの仕組みです。
上記のような変形結果の$\mathbf{m}$の形を教えてもらえば、たしかに式展開をするとそのような変形が成り立つことまでは確認できるのですが、なんでうまくいくのかよくわからないし、他の設定(例えば、$\mathbf{d}$に1要素追加してみるとか)での$\mathbf{m}$の具体的な計算式をどのように求めればいいのか、よくわかりません。なんともスッキリしません。
スッキリしませんが、andravin/wincnn: Winograd minimal convolution algorithm generator for convolutional neural networksのスクリプトを使えば具体的な計算式を求めることはできますので、誰でも簡単に(?)実装はできます。(そもそも、畳み込みを自分で実装する機会はそうそうないですが。)
なお、計算式を求めるためには、Chinese Remainder Theoremという定理を使うそうです。
Winogradアルゴリズムとスパース化を組み合わせる
上述のWinogradアルゴリズムはパラメーターの行列をごちゃごちゃと変形するアルゴリズムで、スパース化はパラメーターが0の部分は式を計算しなくていいよね、というアイディアです。この2つのアイディアを組み合わせることはできるでしょうか。
元のフィルタ行列がスパースであったとしても、Winogradアルゴリズムで変形後のフィルタ行列は非ゼロ要素の割合が増えてしまいがちなので、単純に組み合わせるだけでは、効率がよくありません。効率を考えると、変形後の行列をスパースにしたほうが好ましいでしょう。
Liらは、Winograd化してからスパース化とfine tuningを行うことで、ほとんど精度を落とさずに、通常のスパース化されたネットワークよりも計算量の少ないネットワークを作成しました。(Enabling Sparse Winograd Convolution by Native Pruning)
AlexNetをスパースWinograd化することで、0.1%の精度ロスで、これまでよりも計算量を削減できています。ただし、全体としてどれぐらい高速化できたのかは、 depending on the underlying hardware and the quality of implementation であるため we leave the actual implementation for future work として報告していません。Table 1を見る限り、通常のWinogradアルゴリズムで得られるのと同じぐらいの高速化が可能なように見えます。
この論文の著者は全員がIntel所属で、Intelはスパースに力を入れてるなと言う雰囲気を感じました。
低ランク近似
畳み込み計算は、データ側をim2col(loweringとも言う)という操作で展開してやると、行列積に変形できます。im2colと行列積では、圧倒的に行列積の方が計算コストが高いので、行列積の計算を近似で済ませよう、というアイディアが出てきます。フィルタ側の行列をあらかじめ低ランク近似することで、高速化できます。
Dentonらは、SVDを使ってパラメーターの行列を分解してから低ランク近似することで、1%程度の精度の低下と引き換えに、2倍程度の高速化が可能であることを示しました。(datasetはImageNetで、ベースのネットワーク構造は多分AlexNetです。)(Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation)
最近の$3x3$畳み込みを多用するネットワークが低ランク近似で高速化できるのか、ちょっと気になります。
辞書分解
Bagherinezhadらは、フィルタ$\mathbf{W} \in \mathbb{R}^{m \times w \times h}$を辞書ベクトル$\mathbf{D} \mathbb{R}^{k\times m} $の重み付き和で表現することで、畳込みをそのまま計算するのではなく、まず辞書と入力ベクトルの畳み込みを計算してその重み付き和で取るという近似手法を提案しました。どれぐらい元の畳込み計算をうまく近似できるかは辞書サイズに依存しており、その点、低ランク近似とアイディアとしては似たところがあるように感じます。
AlexNetをベースネットワークとした実験では、1%程度の精度低下で、3倍程度の高速化が実現できたそうです。
LCNN: Lookup-based Convolutional Neural Network
depthwise separable convolution
畳み込みニューラルネットは一般的には、入力チャンネルと出力チャンネルの間で総当たりでフィルタ処理を実行します。つまり、入力チャンネル数が$m$で出力チャンネル数が$n$であるとすると、この段階でもう、計算量が$O(mn)$です。入力画像サイズを$w \times h$として、畳み込みカーネルサイズを$k \times k$とすると、畳み込みレイヤーの計算量は$O(mnwhk^2)$になります。
ここで、separableという概念が出てきます。例えば、ガウシアンフィルタをナイーブに実装すると、半径を$r$として、$w \times h \times r^2$の計算量がかかりますが、実は、縦方向のフィルタと横方向のフィルタを2回実行するだけで同じ結果を得ることができるので、$w \times h \times 2r $の計算量で実現することができます。半径が大きくなればなるほど、この計算量の差が効いてきます。ここでのseparableとは、フィルタを縦方向の計算と横方向の計算に分離可能である、という意味だと思って良いでしょう。
depthwise separable convolutionでは、チャンネル方向の畳み込み計算の総当たりをやめて、畳み込みを2ステップに分割します。1つ目のステップでは3x3チャンネル方向の総当たりを行わず、2つ目のステップでは1x1の総当たりを行います。
言葉でゴチャゴチャ説明するよりも、図を見た方が早いでしょう。下図の左側が通常の畳み込みのイメージ、右側がdepthwise separable convolutionのイメージです。入力は上から来て、下側に出力するものだと考えて下さい。○が1つのチャンネルを表していますので、入力が3チャンネル、出力が2チャンネルという設定になります。太字が3x3の畳み込みを、細字が1x1の畳み込みを表現しています。
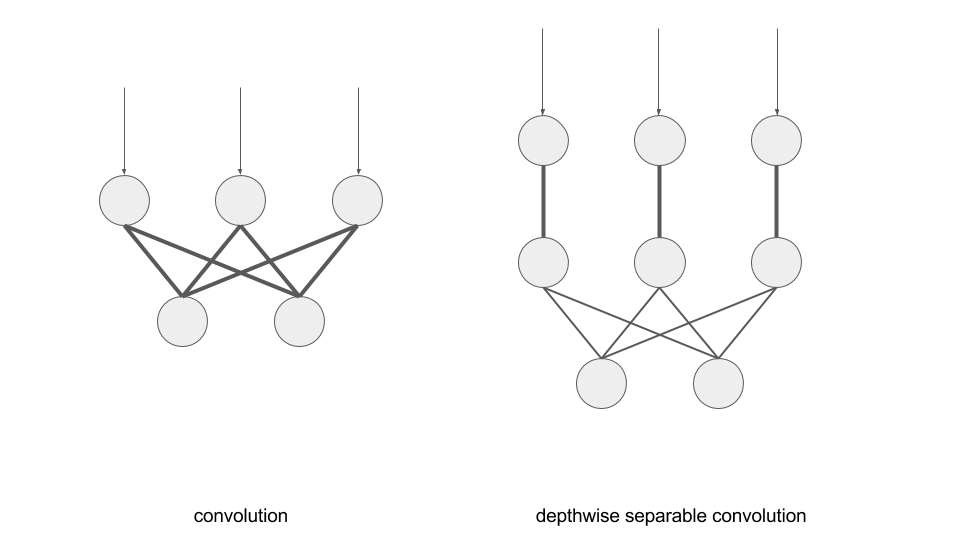
このように、もともとの入力チャンネルx出力チャンネルでの総当たりでの畳込み計算を、空間に対する畳込み(例では1段目の3x3の畳み込み)とチャンネル間の相互作用を表現するための1x1の畳み込みに分けることで、計算量を大幅に減らすことができます。ガウシアンフィルタの場合と違い、separableではないものをむりやりseparateしているのだという点は、ちょっと注意したほうがいいかもしれません。
depthwise separable convolutionは、XceptionやMobileNetsで使われており、最近、注目を集めています。
ただし、depthwise separable convolutionはそんなに速くないんじゃないかという報告もあります。そんなに速くないどころか、むしろ通常の畳み込みレイヤーよりも大幅に遅くなってしまっている場合すらあります。
遅くなる可能性としては、CUDAのカーネル呼び出しのオーバーヘッドと、im2colの重複が挙げられます。まず、前者についてですが、TensorFlowのdepthwise separable convは、入力チャネル数分だけ普通の畳み込みのカーネルを呼んでいます。PyTorchも同様です。CUDAのカーネル起動は約2.5マイクロ秒程度のオーバーヘッドがあるそうなので、入力チャネルが64だとすると、カーネルを起動するだけでも0.16ミリ秒のオーバーヘッドになります。1レイヤー辺り0.2ミリ秒以下のオーバーヘッドなので、これが支配的な要因ではなさそうです。
次に、im2col(lowering)について検討しましょう。こちらの論文に書かれた時から実装方針が変わっていないならば、cuDNNはタイル単位でim2colして行列積の形で畳み込み計算をしています。これまではim2colは1回だけだったのに、同じデータに対してim2colを64回も呼び出すことになるので、そちらがボトルネックになって元のconvolutionより遅くなる可能性は十分にあるでしょう。
ということで、どうにかしてim2colの重複計算をなくさないと、速くならないんじゃないかなと推測します。Chainerだとim2colのあたりもPythonで比較的簡単に触れるので、Chainerに詳しい誰かが実験してくれないかなぁ。
こんな推測を長々と書いて、もう最新のcuDNNだとim2col使ってないよ、全然見当ハズレの予想だよ、なんてオチだったら恥ずかしいので、そういうときはこっそりDMとかで指摘してください。
複数のレイヤーを融合する
典型的な畳み込みネットワークでは、畳み込み、非線形関数、畳み込み、非線形関数、みたいな感じで交互に計算を繰り返します。畳み込み計算は中間データ量が大きくなりがちなので、計算前後のデータをメモリに転送する部分のコストも馬鹿になりません。そこで、複数の畳込み計算を融合して効率してやろう、というアイディアが出てきます。このように、複数のレイヤーを融合して、中間データをメモリに書き出さずに計算する手法をlayer fusionと呼びます。
簡単のために、まず、3x3の畳込み計算(paddingは上下左右に1ずつ取る, strideは1)だけを2回繰り返す場合を考えましょう。3x3でpadding=1, stride=1だと、畳込み計算の前後で画像サイズが変化しませんので、説明が少し簡単になります。
入力ベクトルを$\mathbf{x} \in R^{3 \times w \times h}$とし、以下のように畳み込み関数$f_1$, $f_2$を適用するものとします。
$$ \mathbf{h}_1 = f_1(\mathbf{x}) $$
$$ \mathbf{h}_2 = f_2(\mathbf{h}_1) $$
$\mathbf{h}_2$における、i番目のチャンネルの(j,k)という位置の値を計算するためには、$\mathbf{h}_1$における、(j,k)の周囲を囲む3x3ピクセルの情報が(全チャンネル分)必要になります。もう1レイヤー前をたどると、$\mathbf{x}$における、位置(j,k)における5x5ピクセル分の情報が必要になります。逆に言うと、それ以外の部分の情報は必要ありません。
単に$\mathbf{h}_2$の値を計算したいだけならば、$\mathbf{h}_1$の値をメモリ上に保存する必要はないので、$\mathbf{x}$の位置(j,k)の周囲5x5ピクセル分の値だけを切り取ってきたものを$\mathbf{x}_{25}$とすると、次のように書けます。
$$\mathbf{h}_{2, i, j, k} = f_2(f_1(\mathbf{x}_{25}))$$
ただし、$\mathbf{h}_{2, i, j, k}$は$\mathbf{h}_2$における$i$番目のチャンネルの$(j,k)$という位置の値を指すものとします。このように$\mathbf{h}_2$をダイレクトに計算すると、メモリアクセスを減らすことができます。
メモリアクセスの回数が減るだけなので、メモリバンド幅がボトルネックになっているか、メモリキャッシュミスが頻繁に起きていて演算器に十分にデータが届いてない、みたいな状況でなければ高速にはなりませんが、実際、 AlwaniらがAlexNetの1層目と2層目を融合したところ、CPU実装では2倍程度の高速化ができたそうです。
もっとも、上記の説明通りの単純な実装では、計算の重複が増えて、かえって遅くなってしまいます。重複計算をしないためには、計算した結果を一時的にキャッシュメモリに保存しておく必要がありますが、どういう順番で計算して、どの部分のキャッシュをいつ消すのか、考え出すと頭が痛くなりそうです。
まとめ
畳み込みの計算自体を高速化する手法や、畳み込みニューラルネットの構造自体に手を入れて高速化する手法など、とにかく、畳み込みニューラルネットを高速にする手法を紹介しました。
ロボホンがすれ違い顔認識機能を搭載するというニュースを最近見ましたが、他にも、周辺環境を認識し続ける機械は、これから増えていくでしょう。電車の中にカバンを忘れそうになったら、スマホかなにかが警告してくれる。一度名刺交換した人の名前を忘れても、スマホかなにかが教えてくれる。そんな時代が近づいてきています。
そのためには、消費電力を減らすことが大きな課題になります。高速化ができれば、その分クロックを落とすなりスリープするなりできるので、消費電力の低減にも直結します。
スマートニュースは、これからも高速化に注目していきます。