こんにちは。スマートニュースの高橋力矢です。弊社も含む多くの企業の内側では、短期の利得を重視した施策と、将来に大きな利益を生み出すと考えられる施策との間でどのように資源を割り振るべきか議論が発生します。判断基準が曖昧になりがちなこの短期・長期視点について、数理科学からの観点を紹介したいと思います。

強化学習に代表される賢い人工知能の一つの特徴は、長期最適な意思決定ができることとされており、その背後には将来の利益を一貫した割引率で割り引く指数割引 (exponential discounting) があります。指数割引は会計や株式投資において企業価値を見積もるディスカウント・キャッシュフロー (DCF) 法にも採用されます。例えばお金であれば、今の金利が2%だった時、100ドルを銀行に預けると一年後に102ドルになります。一年後に手に入る100ドルだったら100 / 1.02 = 98.03 [ドル]の現在価値しかないわけです。年利を$100r$ [%]として $t$ 年後の収益$V$は現在価値にすると$V(1+r)^{-t} \equiv V\exp(-\log(1+r)t)$ですね。金利が定数ならば割引関数が時間の指数関数として表現される点から、指数割引と呼ばれています。

一定金利という仮定に疑問を持たれた方は良い目を持っています。心理学や認知科学の分野では、人間を含む生物が指数割引ではなく双曲割引 (hyperbolic discounting) を採用していることが実験的に示唆されています。双曲割引では $t$ 年後の収益を$V(1+\lambda t)^{-\alpha}$ のようにべき乗で割り引きます。$\alpha=1$の場合は反比例の双曲線を描くので双曲割引と言うわけです。数式そのものよりも示唆の方が重要です。双曲割引は遠くの将来でもそれほど減衰させないが直近は大きく減衰させる、という変わった性質を持っています。この特質は、煙草やアルコールが有害だとわかっているのにやめられないといった「言ってたことや考えていたことと、実際にやっていることが違う」状況をうまく説明できます。双曲割引は不合理な意思決定方法とされており、何故なのかは説明の一例を後述します。

長い進化を経て生き残ってきたはずの生物の生存戦略が、「不合理な」意思決定方法になっているというのはちょっと不思議です。果たして双曲割引法は本当に不合理な意思決定手法なのでしょうか? あるいは強化学習を含む人工知能アルゴリズムは本当に指数割引のままで良いのでしょうか? 関連研究を紹介しつつ、この辺りのモヤモヤしたところを議論してみたいと思います。

合理的な近視眼または合理的な長期思考

「あの人は近視眼的で目の前の利益にしか目が向かない」「あの人は長期思考で投資により直近の損を出した後で将来大きなリターンを回収する」などといった言い方を見かける方もいるでしょう。前者に不合理的、後者に合理的というラベルを振る人がいますが、意思決定理論ではそのような分類は正しくありません。

数理的な観点からは、近視眼的かつ合理的な人が存在しえます。例えばアルコールをやめられない人にとって、本日お酒を飲むことで得られる快楽が100ポイント、そのお酒により翌日以降に来る二日酔いや体の不調によるダメージがマイナス150ポイントだったとしましょう。もし1日当たりの割引率が1/1.6=0.625で一貫しているのであれば、お酒を飲むことの割引現在価値は100 - 150 / 1.6 = 6.25 [ポイント]、お酒を飲まないことのそれは0ポイントでお酒を飲んだ方が報酬現在価値が高く、お酒を飲むべきだという結論になります。

近視眼的合理性は著名な経済学者のGary S. Beckerらが提唱したrational addictionにあたります。アルコール依存症から抜けないのは、その本人の割引率が1よりもかなり小さく直近を重視している価値観の問題であって、本人がそう望んでいるのだから他人がとやかく言うことではない、という見方です。そしてアルコールに依存しない人は割引率が1に近く将来を重視する長期性・合理性を持っているので、その人の選択もまた価値観として尊重されるべきという含意になります。

割引率が時間不変の世界には、合理的な短期思考の人と合理的な長期思考の人だけがいます。例えば3年後に手に入る30ドル (Option A) と9年後に手に入る80ドル (Option B) を比較するときに、短期思考の人は図1左のように、長期思考の人は図1右のように割り引きます。この両者のどちらも実際のところ合理的です。なぜなら、どの時刻においてもOption AとOption Bの魅力の順序関係が不変で価値観と行動が一貫しているからです。短期思考の人にとってはすぐ手に入る3年後の30ドルが一貫して(どの時刻においても)魅力的であり、長期思考の人にとっては80ドルが一貫して魅力的です。

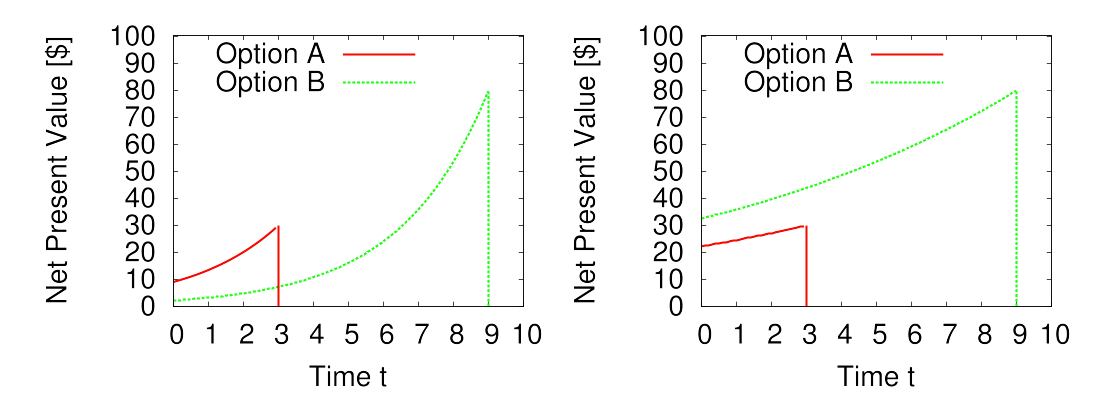
図1. 指数割引: 短期報酬を重視(左) / 長期報酬を重視(右)

一貫しない割引率による不合理性

Rational addictionで物事を片付けてしまうと不合理的な人は存在しませんし、他人がとやかく言うなという結論で終わってしまいます。本当に不合理な人は存在しないのでしょうか? その答えのヒントはアルコール依存症の人が口にするメッセージにあります。彼らは「アルコールをやめたい」と口にします。しかし目の前に酒瓶があると開けて飲んでしまいます。彼らは自分の希望を実現できていません。望む目標がありながらそれを実現する行動が取れない状況は、不合理と呼べるのではないでしょうか。

異時点間の選好逆転

生物は不変ではなく時間依存した割引率を使っており、べき関数が当てはまりやすいことを冒頭で述べました。指数関数ではなくべき関数で割り引きを行うとどうなるか、図1と同じ3年後30ドル or 9年後80ドルの選択で示したのが図2です。図2左が全期間を示しており、そのうち直近将来3年間を拡大表示したのが図2右です。拡大期間をみると、今現在においては将来の80ドルの方を直近の30ドルよりも高く評価していることがわかります。ところがこの大小関係は1.5年目付近で逆転しており、2.5年目や3年目においては直近の30ドルが魅力的に見えています。このことから何が起きると示唆されるでしょうか?

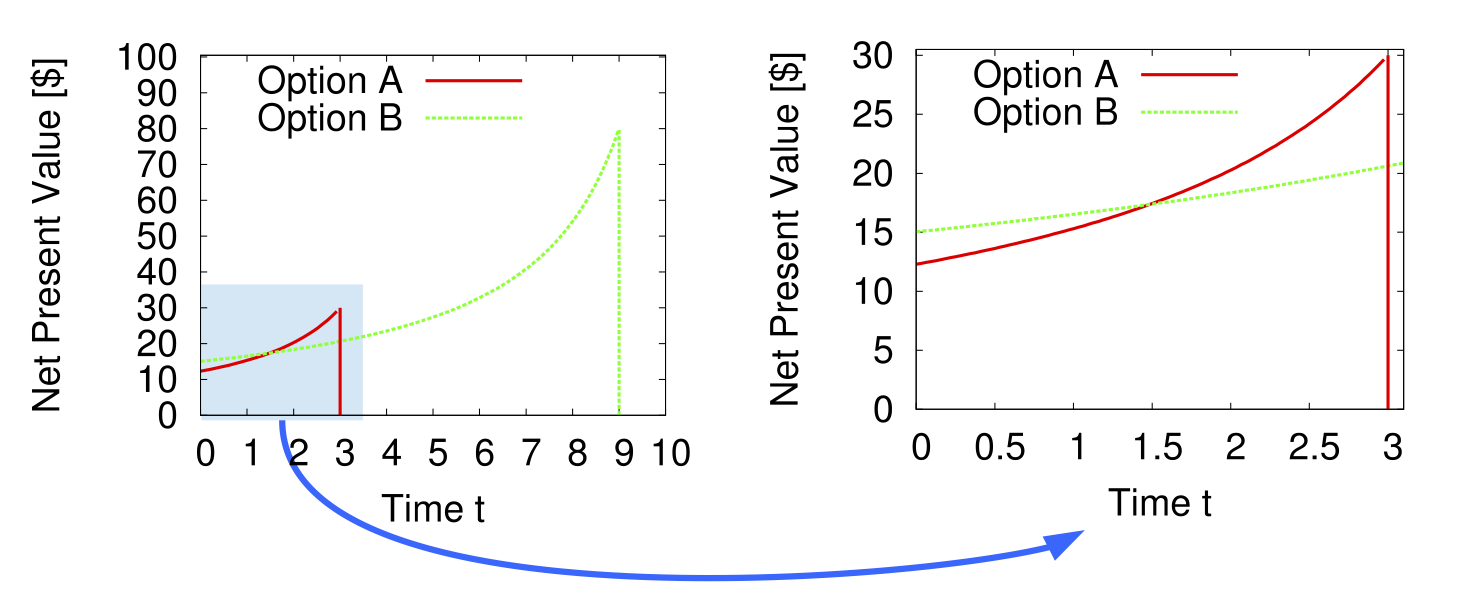
図2. 双曲割引: 全体(左) / 直近の選好逆転を拡大表示(右)

発生するシナリオは次のようなものです。まず今日現在、30ドルと80ドルの選択肢のどちらを選んでもすぐにお金は手に入りません。ただ少なくとも、この人の頭の中では将来の80ドルの方が魅力的でそちらを選ぼうという「長期思考」が働いています。ところが今から1.5年が経過した時点で、あと1.5年すれば手に入る30ドルの方が魅力的に見えてしまい、急に近視眼的に変わってしまうのです。3年目になった時点では直近の30ドルの魅力は将来の80ドルを遥かに凌駕しており、この人は30ドルを選び80ドルを諦めてしまいました。十分に昔なら将来のより大きな利益を優先する長期「思考」が出来ていたはずなのに、いざ選択肢が目の前にやってきたら近視眼的で衝動に負ける人に変わってしまったのです。

この近視眼的選択と長期的選択の間の選好逆転は双曲割引の顕著な特徴です。アルコールが目の前にないとき、すなわち距離的/時間的に十分離れているときはアルコールをやめようと「思っている」(=長期的選択を選んでいる)のに、いざ目の前に来ると誘惑に負ける(=近視眼的選択を選ぶ)という依存症は、双曲割引による選好逆転によって説明できます。

双曲割引する人からはお金をむしり取れる

双曲割引は他にも不合理な性質を持っています。わかりやすい例は、双曲割引している人からは何も対価を払わずにお金をむしり取ることが出来てしまう、というものです。お金をむしり取る行為をMoney pump (Cubitt & Sugden, 2001)と言います。図2右の拡大結果を眺めながら次のステップを追ってみてください。仮に最初に被験者がOption Aを保持していたとして、我々は彼をカモにします。

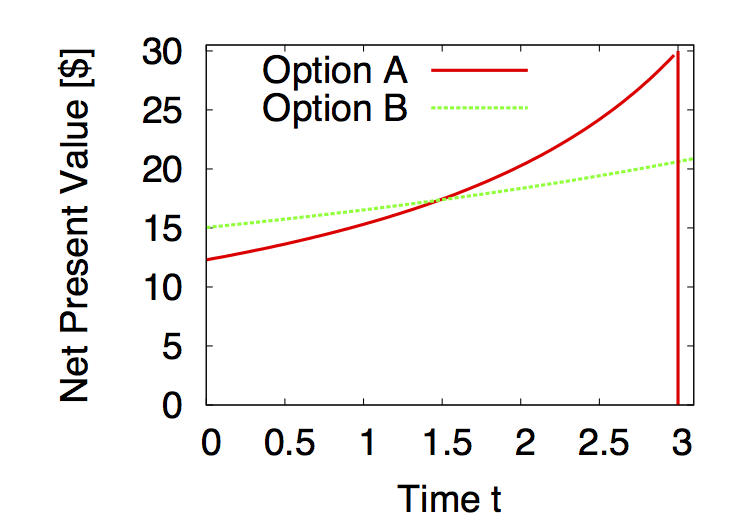
図2右再掲. 直近の選好逆転を拡大表示

  • 時刻 $t=0$: 私たちは誰かからOption Bを借ります。そして被験者に対して、そのOption Bと彼の持つOption Aを手数料つきで交換しようと提案します。彼は長期的なOption Bの方が価値があるとみなし、現在価値にして15 - 12.5 = 2.5 [ドル]の支払いに同意します。こうして私たちはOption A - Option B + 2.5ドル, 彼はOption Bを保有するようになりました
  • 時刻 $t=3$: 私たちは再び被験者に近づき、私たちのOption Aと彼のOption Bを手数料付きで交換しようと持ちかけます。彼は今すぐ金に交換できるOption Aの虜に変わってしまっていますので、手数料として 30 - 20 = 10 [ドル]の支払いに応じます。私たちは手に入ったOption Bをすぐに最初の貸主に返却しました
  • 最終的に私たちの手元には 10 + 2.5 = 12.5 [ドル] + (2.5ドルに対する手数料) - (最初のOption Bの貸料)、彼の元には彼が元から保有していたOption Aが残りました。賃料が高くなければ私たちはノーリスクで金を手に入れることに成功します。しかし彼は結果的に何も得ません

このような搾取は、指数割引する人に対しては成立しません。たとえ近視眼的な人であっても、その人の割引率が時間不変で指数割引している限りは選好が一貫しており、私たちにとっての決裁取引となる再度の交換ができないのです。あなたが近視眼的な人を愚かだと思ったとしても、彼が合理的に近視眼的である(=割引率が1よりかなり低い指数割引を行う)限り彼を騙すことはできません。

世の中に双曲割引する人が大量にいるなら、Money pumpをいろいろな人に対して繰り返すことで簡単に大金持ちになれてしまいます。双曲割引はこのような搾取に対して無力であり、生物がそのような間抜けな行動を繰り返していたら進化の過程で淘汰されていたはずだと主張する人もいます。

双曲割引の方が合理的なケースもある

双曲割引しているとどのように痛い目に会うかわかったところで、今度はむしろ双曲割引の方が優れている点について紹介したいと思います。

金利の確率的変動を取り入れる

我々の経済では、預金金利や公定歩合は一定ではなく経済状況を反映して変動します。すると金利一定の元で指数割引するのは正しくなさそうです。例えば金融機関の債券トレーダーは金利の変動に由来する資産価格の変動を日々追いかけており、金利変動の予測モデルにも色々あります。

精確に金利変動を予測することをやめて金利が確率的にばらつくだけの大雑把なモデルを考えてみましょう。例えば単位時間あたりの連続複利が$\lambda$である指数割引において、$\lambda$が定数ではなくガンマ分布$Gam(\lambda; \alpha, \tau) \triangleq \dfrac{\tau^\alpha}{\Gamma(\alpha)}\exp(-\tau\lambda)$で与えられる確率変数だったらどうなるでしょうか。その答えは式(1)で与えられる双曲割引です。ガンマ分布のshapeパラメータ$\alpha$がそのままべき指数になります。

$$ \int_0^\infty \exp(-\lambda t) Gam(\lambda; \alpha, \tau) d\lambda \equiv \dfrac{1}{(1+t/\tau)^{\alpha}} ~~~~~ (1) $$

金利がいつ変動するか精確に読めない状況で、確率的に金利変動を考慮するだけでも指数割引はあっさりと双曲割引に変わってしまいます。金利が変動する状況では指数割引の方がむしろ不合理的で、お金を損します(Azfar, 1999)。一定金利が強く仮定できる安定した環境では双曲割引は前述の通り不合理な振る舞いですが、環境の不確実性を考慮した場合にはそれなりにまともな割引法と言えます。

  • 世界的なベストセラーであるブラックスワンの著者であるN. N. Talebは双曲割引を安易に不合理性に結びつける行動経済学の世界観を批判しています
  • 不確実性を考慮した世界での合理性に興味がある方はノート: Silent Riskを読んでみてください

金利を積分するアプローチにおいては、根源的事象としての双曲割引に対しても種々の実験的反論が試みられています。本論から外れるため詳説は省きますが、分布の周辺化について理解している方に以下の参考情報を挙げておきます。

  • 時刻で条件付けされた割引関数と、時刻を周辺化して時刻非依存の割引関数を考える
  • 周辺化された割引関数が双曲割引でも、元の条件つき割引関数は双曲割引でない場合がある
  • 時刻で条件付けしてミクロに見ても双曲割引なのか、それともミクロでは違った意思決定規範が動いているのかについては論争が続いている。例えば (Richards & Hamilton, 2012) を参照
  • この論争における分析は金融市場における資産価格変化率の時系列モデリングと似ている
    • 時刻について周辺化した分布は裾野が重たい分布であるが、時刻による条件付き分布(分散が時間変動)は裾野の軽い正規分布でもある程度は説明できる (Cont, 2001)
    • 分散の時間変動を取り入れる場合であっても、実際には条件付き分布に裾野の重さを取り入れた方が説明能力が高い (Verhoeven & McAleer, 2004)

「超」長期思考の考慮

お金のように明確で客観的な金利がない状況の場合、適切な意思決定方法は金利変動の場合よりも難しいでしょう。しかし未来と現在に同じ獲得や損失がある場合に現在の値を高く評価すべきなのは確かです。そうでないと、下記のようなおかしな意思決定が可能になってしまいます。

  • 地球が何十億年か先に太陽に飲み込まれて死ぬことは確定している
  • 割引率が1なので、数十億年先に全滅するのも今全滅するのも同じだけのダメージである
  • したがって我々は今の時点で他の惑星への移住計画に全ての経済力・資源を集中すべきである

極めて先の将来を評価するとき、事前に割引率を固定する指数割引は不便です。例えば気候変動の問題に対処するために炭素税をいくらにすべきか、自動車の排ガス規制をどの程度にするか考えるとします。このとき割引率を100年で半減する値 (連続複利なら$\lambda = -log(0.5)/100 \equiv 6.93 \times 10^{-3}$)にすれば良いでしょうか。これだと1,000年先の人類の損失については何も考慮してくれません (その影響は$0.5^{10} = 9.76 \times 10^{-4}$で端数でしかありません)。では1,000年で半減させれば良いのでしょうか。すると10,000年先は考慮しません。また単に半減期を長くしていくだけだと、直近の痛みを軽視して経済活動を制限しすぎてしまいます。

一方で双曲割引のべき減衰は指数減衰よりも裾野がずっと重たいので、超長期の影響もそれなりに取り入れてくれます(Farmer & Geankoplos, 2009)。気候変動への対処のように、遠い先の人類の幸福を考慮した意思決定問題に関しては双曲割引がより適切です。気候変動に関して言えば、大気汚染の度合いによる人々の主観的な幸福度と、お金で図られる経済活動による客観的な獲得/損失に関して区別して異なる減衰関数を用いるアプローチも検討されています(Goulder & Williams, 2012)。この方法論では両者とも双曲割引を使いつつ、かつ式(1)における$\tau$を幸福度とお金とで異なる値に設定するようです。

双曲割引の弊害を乗り越えて逆手に取る

双曲割引は報酬の種類(e.g., お金, 食べ物)に依存しないユニバーサルな現象であるがゆえに、双曲割引傾向のある人は様々な問題を同時に多く抱えており、下記の項目はその代表例です。例えば肥満の人は健常者よりも大きな債務を抱えているという統計があります(Guthrie & Sokolowsky, 2014)。

  • アルコールや煙草の依存症: 長期的にはやめたいと考えているが目の前にあると摂取してしまう
  • 肥満: カロリーの摂りすぎが長期的に悪いとわかっても目の前に食べ物があると食べてしまう
  • 借金中毒 (e.g., 多重債務者): 金利による将来の負担が頭ではわかっても、目の前に札束をちらつかせられると消費誘惑に負けて大きな金利負担を背負ってしまう

この状況を打破するためには、短期報酬が得られる選択肢を強制的に排除することも必要です。双曲割引傾向が強い人にはお金を貸さないこと、リスクの高い金融商品は提示しないことも大事です。彼らに対する食事プランは食べ放題ではなくて一定量だけが出てくるコースから選ばせるべきでしょう。例えば広告ビジネスにおいても、目の前から近視眼的な誘惑を排除する必要性は出稿戦略(時間帯、オーディエンス)に反映すべきですし、一部のTVコマーシャルの露出時間帯が規制されているのは、双曲割引する消費者をターゲット視聴者から除外するためのヒューリスティックです。

規制というとビジネスが制限されることばかり想像されがちですが、短期誘惑を排除するシステムはむしろ経済的には大きなリターンにつながります。先ほどのMoney pumpに見られるフリーランチを社会的に有益な形で手に入れるのです。一般的に言って、純粋にお金の増大を目的とする経済主体と、双曲割引の誘惑から逃れたい消費者との間にはwin-winの取引が成立しやすくなります。例えば、定期預金のように一定期間資金を引き出せない預金口座が、低金利でも役に立つことがあります(Thaler & Benartzi, 2004)。お金を目の前に置かないことで、双曲割引のむしろ長期思考面を発揮して消費衝動から逃れることができます。このような制限された口座は、銀行に対しては低い調達金利を提供する一方で、預金者は双曲割引による使いすぎを防いで貯金を増やせるという面白いwin-win取引を生み出します。

合理的だけど脆弱な経済人

指数割引は、金利が一定であることを仮定できる場合のみに合理的であって、環境の変化に対しては脆弱な意思決定規範です。金利が将来どう変化するか精確な予測ができるなら特殊な割り引き方も考えられますが、どう変動するかわからないなら確率的にぶらして「大雑把に双曲割引する」のも悪くないように見えてきます。特に離れた時点における長期思考の優先は大事な性質です。とはいえ、代償としての近視眼性をどうするかは考えものです。

指数割引にせよ、不変の効用関数による選好にせよ、一貫した選択規範に基づいて行動することでその人から搾取することができない点は、その人の経済的合理性とみなされます。しかし効用関数が時間的に整合して不変であることに、どれほどの価値があるかは疑問です。そのような「石頭」の人がたくさんいても、あまり社会が良い方向に動かない気がします。商品の選択であれば、画期的な新商品の登場によって今まで重視していなかった側面を重視するように消費者の嗜好が変わっていいはずです。

金利の変化、効用関数の変化に関する可能性を確率的に表現して積分したり統計的推定と対応させる枠組みによって、より優れた意思決定方法があり得ると私は考えています。気候変動問題に対処する際の双曲割引の積極的利用はその一例です。意思決定メカニズムを考えるにあたっては、何が定数で何が確率変数であるか、どこに不確実性がのっているのか検討するのが大事です。そして仮定が変わると合理的な規範も変わってしまうので、完全に合理的であることよりも仮定の変化に対して頑健であることを優先させたメカニズムを考えるのが良いと思っています。

まとめとオススメ書籍

今回は、双曲割引というシンプルな数式が生み出す奇怪な現象を味わって頂きました。経営会議で、長期目標が大事だと言っておきながら実際には短期のタスクしか手をつけていない、という事態に自社が陥っていないか参考にしてみてください。あるいは子育てのように、子供が育った将来において大きな喜びがあるものを大事だと言っておきながら、実際には仕事によって確実に手に入る明日の給与や成功体験に目が眩んでないか考えるのも良いでしょう。

そして一見不合理な双曲割引が、環境の変化まで考慮すると石頭の指数割引よりもマシである可能性に言及しました。割引率の確率的変動について、強化学習コミュニティでも深く検討して良いと思います。

最後に、私が双曲割引を知るきっかけとなった一冊の本を紹介したいと思います。George Ainslieの誘惑される意志で、日本では2006年に出版されました。当時、行動経済学は日本では全く流行っていませんでしたし私も馴染みのない分野でした。しかし出版直後の本書を書店でたまたま見つけたときは、翻訳が山形浩生さんだったことも手伝って大変気になり、すぐに買って読破してしまいました。その中身に虜になって関連分野を調べ始めたことが、私が行動経済学と機械学習の統合を考え始めるきっかけであり、その後の研究キャリアに大きく寄与しました。ですから、流行ってないことでも光っている何かを見つけたらすぐに自分の糧にすることをお勧めします。興味がある人はこの「誘惑される意志」もぜひ手にとってみてください(会社ブログなので宣伝手数料を頂けないのが非常に残念です 笑)。

References