株式会社ゴクロの中路です。
以前のベイズ分類をベースにしたSmartNewsのチャンネル判定で触れたように、SmartNewsで配信する記事を「スポーツ」「エンタメ」「コラム」のようなチャンネルに分類しているのは、人ではなく機械です。そのアルゴリズムとして前回ご紹介したのは「ナイーブベイズ分類器」ですが、記事の分類を行う手法は、他にも様々なものがあります。その中で今回はLatent Dirichlet Allocation(以下LDA)について、先日東京大学の博士課程の皆さんと、社内で合同勉強会を行った際に作成した資料をベースにご紹介します。
LDAでできることの例
前回ご紹介したナイーブベイズ分類器を構築する際には、すでにトピックのラベルが付けられた文章を、学習データとして用意する必要がありました。一方、LDAの場合は、
- 東京でサッカー大会が開催された。xx選手のゴールが圧巻であった。
- 先日行われたゴルフの試合で、今シーズン発のホールインワンがあった。
- サッカー日本代表xx選手の移籍報道が加熱。移籍金はいくらになるか。
といったトピックのわかっていない記事の集合のみが与えられているときに、
のように単語をクラスタリングしたり、
トピック1:
- 東京でサッカー大会が開催された。xx選手のゴールが圧巻であった。
- サッカー日本代表xx選手の移籍報道が加熱。移籍金はいくらになるか。
- 先日行われたゴルフの試合で、今シーズン発のホールインワンがあった。
- 文書のクラスタリングに関しては各トピックごとに分かれるというよりは「文書の背景のトピックの混ざり具合がわかる」というのが、より適切な表現かもしれません。
- LDAだけを用いて、トピック1、トピック2に「サッカー」や「ゴルフ」といった、トピックの命名を行うことはできません。
LDAの概要
モデル
ここでは、LDAにおいて文章の生成がどのようにモデル化されているか、について書きます。LDAでは、文章の背景には、”トピックの混合率”が存在すると考えます。例えば下のような「トピック1が10%、トピック2が70%、トピック3が20%混ざった文章」を考えます。
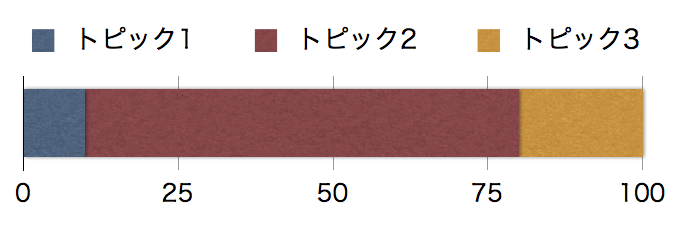
文章の背景にあるトピック分布
文章中の各単語の背景には、一つのトピックが存在すると考えます。各単語の背景トピックは、文章の”トピックの混合率”に従って生成されます。上でトピック2の割合が高かったので、下の図でトピック2の割合が高くなっています。
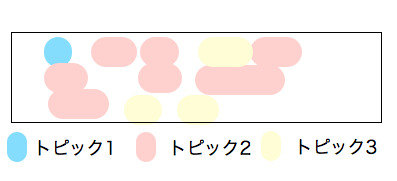
単語の背景のトピックが決まっている文章
各単語は、その背景のトピックに従って生成されます。例えば下の図だとトピック2は野球系の単語を生成する確率が高いことがみてとれます。

単語があてがわれた文章
まとめると、LDAでは文章を 「まずトピック混合率というものがあり、その混合率に従って各単語の背景トピックが生成され、その単語の背景トピックに従って単語が生成されている」 とモデル化しています。
クラスタリングの大まかな手順
文章の集合があたえられたときに、まず各文章の各単語の背景トピックを推定します。一旦各文章の各単語の背景トピックが推定できてしまえば、例えば背景に「トピック2」を持つような単語というのはどういうものなのかをみることで、「トピック2っぽい単語」というのが分かるので、「トピック1っぽい単語」「トピック2っぽい単語」「トピック3っぽい単語」に分けることができる、つまり単語をクラスタリングすることができます。また、各文章にあらわれる背景トピックの数をみれば、「トピック1っぽい文章」等々も同様にわかるので、文章をクラスタリングすることもできます。LDAを用いたスポーツ記事中の単語クラスタリング
以下のスライドでは「LDAを用いたスポーツ記事中の単語クラスタリング」についてまとめました。最終結果をみると、単語が各テーマごとに綺麗に分かれていることが見てとれると思います。
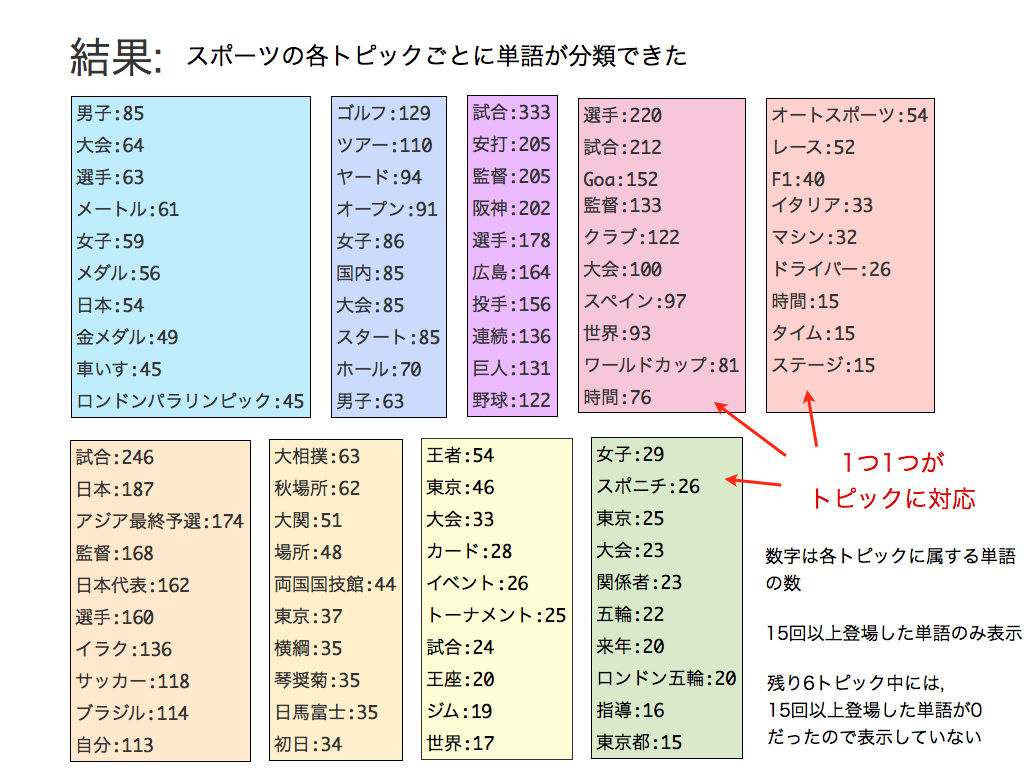
スライド中では触れていませんが、例えば
- 記事中に出てくる単語の背景トピックを各トピックごとに集計
- 最も数が多いトピックを、その記事のトピックと認定
補足: LDAの定式化
ここでは、LDAのモデルを定式化します。少しごちゃごちゃするので、ここは読み飛ばしてくださっても構いません。記号
まず、以下のように記号を定義しておきます。
| 記号 | 定義 |
|---|---|
| $ i $ | 文章のナンバー( (1〜M) ) |
| $ j $ | 各文章における単語のナンバー $ (1〜N_i) $ |
| $ k $ | トピックのナンバー$ (1〜K) $ |
| $ l $ | 単語のナンバー$ (1〜L) $ |
| $ \theta_{ik} $ | 文書iの背景にある混合率のトピックkの成分(例えばトピック1の混合率が10%なら、$ \theta_{i,トピック1}=0.1 $ ) |
| $ z_{ij} $ | 文章iのj番目の単語の背景トピック |
| $ w_{ij} $ | 文章iのj番目の単語 |
| $ \phi_{kl} $ | 背景トピックがkのときに単語lが生成される確率 |
| $ \alpha_k $ | 背景トピック混合率に関するハイパーパラメータ |
| $ \beta_l $ | 単語生成率に関するハイパーパラメータ |
確率分布
$ \theta_{ik} $ などをまとめて$ {bf \Theta} $などと書くと、 ハイパーパラメータを$ {\bf \alpha}$, ${\bf \beta}$と設定したとき、 トピック混合率が$ {\bf \Theta} $で、単語生成率が$ {\bf \Phi} $で、各単語の背景トピックが$ {\bf Z} $であるような文章群$ {\bf W} $が得られる確率$P({\bf \Theta}, {\bf \Phi}, {\bf Z},{\bf W} |\alpha,\beta)$は以下のような図(グラフィカルモデル)によって表現され、
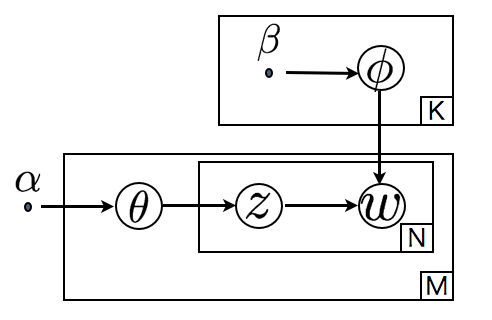
実体は、
$$ P({\bf \Theta}, {\bf \Phi}, {\bf Z},{\bf W} |\alpha,\beta) = \left( \frac{prod_{k}\Gamma(\alpha_k)}{\Gamma(\sum_{k} \alpha_k)} \prod_{i,k}\theta_{ik}^{\alpha_k-1} \right) \left( \frac{\prod_{l}\Gamma(\beta_l)}{\Gamma(\sum_{l} \beta_l)} \prod_{k,l}\phi_{kl}^{\beta_l-1} \right) \prod_{i,j} \left( phi_{z_{ij}w_{ij}} \theta_{iz_{ij}} \right) $$
$$ \sum_k \theta_{ik} = 1 ({\rm for\ all\ }i) ,\sum_l \phi_{kl} = 1 ({\rm for\ all\ }k) $$ となります。$\Gamma(x)$はガンマ関数で、$ x $が整数のときは「$Gamma(6) = 5! = 5 * 4 * 3 * 2 * 1$)」のように階乗に一致する、階乗を実数に拡張したような関数です。
期待値
$ Z $と$ W $が決められているときの$ \theta_{ik} $の期待値は、
$$ \left< \theta_{ik} \right> = \frac{\int d\Theta d\Phi \theta_{ik} P({\bf \Theta}, {\bf \Phi}, {\bf Z}, {\bf W} |\alpha,\beta)}{\int d\Theta d\Phi P({\bf \Theta}, {\bf \Phi}, {\bf Z}, {\bf W} |\alpha,\beta)} = \frac{N_{ik} + \alpha_k}{\sum_{k^{‘}}(N_{ik^{‘}} + \alpha_{k^{‘}})} $$ となります。$N_{ik}$は文章iに含まれる背景トピックkの数です。
また$ Z $と$ W $が決められているときの$ \phi_{kl} $の期待値は、 $$ \left< \phi_{kl} \right> = \frac{\int d\Theta d\Phi \phi_{kl} P({\bf \Theta}, {\bf \Phi}, {\bf Z}, {\bf W} |\alpha,\beta)}{\int d\Theta d\Phi P({\bf \Theta}, {\bf \Phi}, {\bf Z}, {\bf W} |\alpha,\beta)} = \frac{N_{kl} + \beta_l}{\sum_{l^{‘}}(N_{kl^{‘}} + \beta_{l^{‘}})} $$ となります。$N_{kl}$は背景トピックkを持つ単語$l$の数です。
以上2つの式から、(ハイパーパラメータを無視すれば)、文章群$W$が与えられており、その各背景トピック$Z$が定まっているとき、
- 文章$i$の背景にあるトピック混合率としてもっともらしい値は、文章$i$中に含まれている単語の背景トピック数の比と一致する
- トピック$k$が背景にあるときに、「どの単語が生成されやすいか」という単語の生成率としてもっともらしい値は、トピック$k$を背景にもつ全文章中の単語数の比と一致する
もっともらしい$Z$を得る
文章集合$W$が与えられたときの、もっともらしい$Z$を割り出す際、${\bf \Theta}, {\bf \Phi}$については積分してしまって、 $$ P({\bf Z}, {\bf W} |\alpha,\beta) = \int d\Theta d\Phi P({\bf \Theta}, {\bf \Phi}, {\bf Z}, {\bf W} |\alpha,\beta) $$ とすると簡潔です。 (まじめにもっともらしい${\bf Z}, {\bf \Theta}, {\bf \phi}$のセットを割出すということも可能です。)
積分を実行すると、
$$ P({\bf Z}, {\bf W} |\alpha,\beta) = \prod_{k} \frac{\Gamma(\sum_{l} \beta_l)\prod_{l}\Gamma(\beta_l + N_{kl})}{\prod_{l}\Gamma(\beta_l)\Gamma(\sum_{l} (\beta_l + N_{kl}))} \prod_{i} \frac{\Gamma(\sum_{k} \alpha_k)\prod_{k}\Gamma(\alpha_k + N_{ik})}{\prod_{k}\Gamma(\alpha_k)\Gamma(\sum_{k} (\alpha_k + N_{ik}))} $$
となります。
この確率を用いて、例えば$\bf Z$の期待値などの、もっともらしい$\bf Z$の値を計算で求めるのは難しいので、この確率に従う$\bf Z$をたくさん生成して、その$\bf Z$のたくさんのサンプルを使って求めたい量を計算する、という方法がとられます。その際$\bf Z$のサンプルを得るのに用いられる手法がギブスサンプリングです。
詳細は省きますが、ギブスサンプリングを行う手順は以下です。
- まず$\bf Z$の初期値を与えておく。
- $ i, j$をランダムに選ぶ
- 以下の確率に従って$z_{ij} $の値を変化させる。
$$ \begin{split} P(z^{ij} = k|{\bf Z}^{-ij}, {\bf W}, \alpha,\beta) &= \frac{P(z^{ij} = k, {\bf Z}^{-ij}, {\bf W}, \alpha,\beta)}{P({\bf Z}^{-ij}, {\bf W}, \alpha,\beta)}
&= \frac{\beta_l + N_{kl}^{-ij}}{\sum_l (\beta_l + N_{kl}^{-ij})}\frac{\alpha_k + N_{ik}^{-ij}}{\sum_k (\alpha_k + N_{kl}^{-ik})} \end{split} $$( $ l $ は $w_{ij} $ の値、$ N_{kl}^{-ij} $ の肩にある “ $ -ij $ ” は $ z_{ij} $ の分を数えない、という意味です。)
- $ N_{kl}, N_{ik}$の値が収束するまで2, 3を繰り返す。
参考
Latent Dirichlet Allocation([Blei+ 2003]) がLDAの初出の論文で、 Finding scientific topics([Griffiths+ 2004]) がギブスサンプリングを用いた方法の初出です。LDAの背景知識を獲得するために、以下の本が非常に参考になりました。
この通称”PRML本”の総仕上げとしても、LDAは非常によい練習問題であると思います。まとめ
このエントリーでは、LDAを用いて記事のトピックの推定を行う方法と、その簡単な例について書きました。 SmartNewsのサービス向上のために、以上のような機械学習の知見は非常に重要です。日々サービスの改善に努めるだけでなく、今回のような社外の方との勉強会を通じての情報交換も積極的に行っていきたいと考えています。P.S. 株式会社ゴクロでは、SmartNewsの成長を加速してくれるエンジニアを募集しております。興味の有る方は是非ご連絡ください!